This site uses cookies. To see our cookie policy and how to control cookies click hereCookies

Back to Education

Disease spread

using a cellular automaton

In the late 1960's the mathematician John Conway devised the Game of Life (sometimes just called Life). It is an example of a simulation running as a cellular automaton, that is, a grid of cells that can indicate two or more different states. In the original version the cells could be either occupied or vacant. Such constructs can be fun and have interesting mathematics, and, because of their very visual nature, work very well for demonstrating some phenomena.

The example below shows a cellular automaton devised by M Cole that was inspired by the spread of a virus through a population where some number may be immune to infection either through having previously had the infection or through vaccination.

Step 1: The board starts with a population of uninfected people, some of which may have immunity. At the centre is a single person that has been exposed to a virus. The cells are colour coded as follows:

Step 2:

Step 3:

Step 4:

Steps 2 to 4 are repeated until no more moves are available.

Dr Peter Rowlett of Sheffield Hallam University has produced a pre-made grid to download and use if you want to play the paper version.

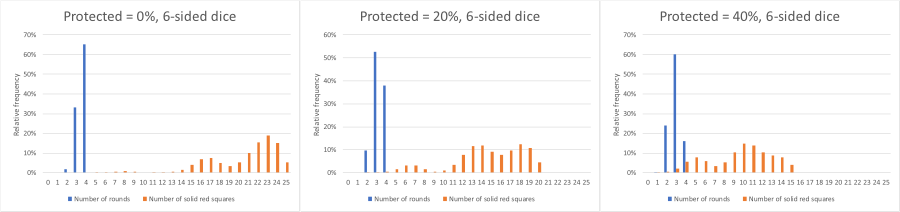
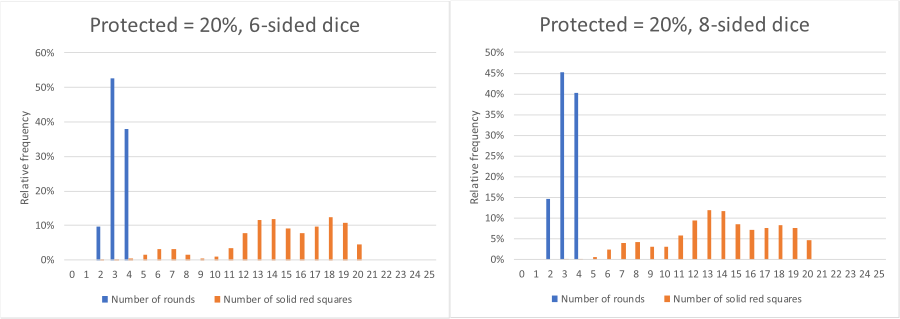
In the original game, the board was a 5x5 grid and a set of six-side dice were used. In the interactive element below, there is a choice of a 5x5 or a 9x9 grid, and a choice of a set of six or eight-sided dice (to allow for all eight neighbours to be infected). All the other rules are the same as the original. The simulation may be stepped through by clicking 'Next', or automatically run by clicking the "Auto" button.

As the outcome is random it makes sense to repeat the game many times to try to obtain some statistics. The original, paper-based game used with a class of students is perfect for this! Of interest would be counting how many complete rounds the game lasts as this is an indication for how long it takes for the epidemic to die out. Also of interest is the number of full red squares left at the end of play as this shows how many people suffered the full disease.

Of course with a small computer program the data analysis can be automated. The results below are shown for the original 5x5 board using six-sided dice. The blue histogram shows the frequency of the game finishing in 1 round, 2 rounds, etc. The orange histogram shows the frequency of the number of full red squares left after play. The diagram clearly shows how both the duration of the epidemic and the number of red squares at the end of play shift to the left, i.e. lower values, as the level of protection increases.

It is noticeable in the above that the orange plot has peaks and troughs. It could be that using six-sided dice causes this as they only allow six out of a possible eight neighbours to be infected. However, running the analysis with eight-sided dice gives a similar outcome, as shown below. It turns out the shape is a side effect of the geometry of the game (non-cyclic boundaries are used).

The plot below shows how the duration of the epidemic falls with the level of protection. Increased protection is clearly effective at stopping the epidemic earlier.

The final plot, below, shows how the number of red squares at the end of play varies with the level of protection. This number is important as it relates to the number of people that have had the full disease and may need care. Clearly as protection increases, the number of red squares falls, but that must be measured against the maximum number of red squares available (remember protected people are coloured blue). The difference between the mean number and the maximum number increases up to 40% protection, after which it falls again, but this is in the context that the number of people who can get infected also falls.

Previous

Next