The game can be played for entertainment. It can also be used to talk about what approaches can be used to solve it - what patterns and rules of placement can you find? Can you produce an algorithm to solve the problem? It can also be used to talk about other mathematical concepts such as "existence" and "uniqueness".
Existence simply asks "is there a solution to the problem?" without necessarily showing this by providing one. This is useful as if there isn't, then no amount of effort will give a successful result and you can save yourself a lot of time. An example of a problem set up with no possible solution is shown below.

In this case the start is at the bottom and the finish is at the top. However, there is a row between the start and finish that states that there are no tiles on that row, and because of this there is no possible way to travel from the bottom to the top. Existence is used in the code behind the game to ensure a viable puzzle is presented.
Uniqueness asks "if there is a solution, is it unique or can there be more than one correct answer?" It can be shown that the answer isn't necessarily unique, as in the example below. This shows two different paths from the start to the finish that also use the correct number of tiles in each column and row.
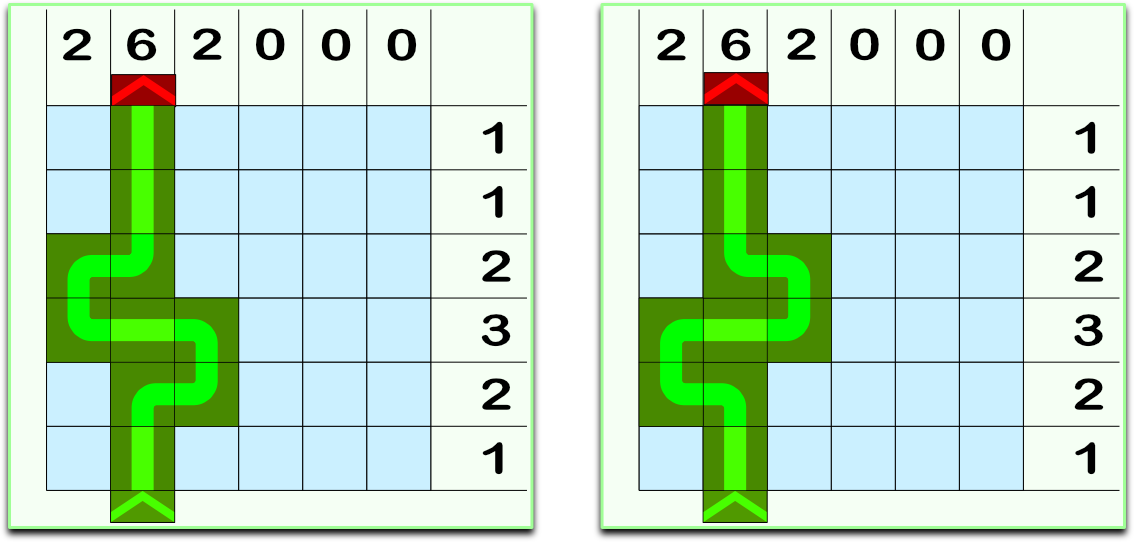
The checking behind the game is kind as it only insists you find a correct path from start to finish, and not the path the computer actually came up with.